揭秘皮亚诺曲线背后的奥秘
皮亚诺曲线是一曲线序列的极限,不再是通常定义下的曲线。下文中"曲线"应解释为"曲线的极限"。只要恰当选择函数,画出一条连续的参数曲线,当参数t在0,1区间取值时,曲线将遍历单位正方形中所有的点,得到一条充满空间的曲线。 皮亚诺曲线是一条连续而又不可导的曲线。
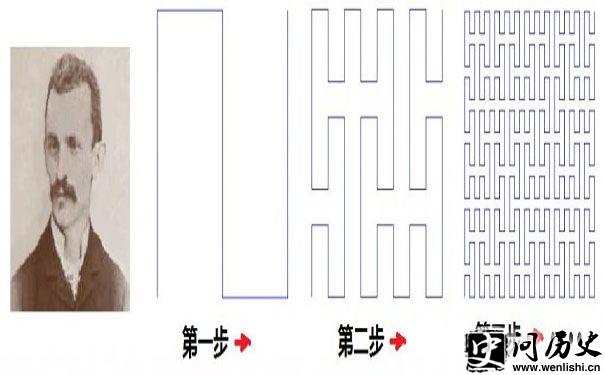
皮亚诺与皮亚诺曲线
1890年,意大利数学家皮亚诺(Peano G)发明能填满一个正方形的曲线,叫做皮亚诺曲线。皮亚诺对区间[0,1]上的点和正方形上的点的对应作了详细的数学描述。实际上,正方形的这些点对于 t∈[0,1],可规定两个连续函数x=f(t)和y=g(t),使得x和y取属于单位正方形的每一个值。后来,希尔伯特作出了这条曲线。
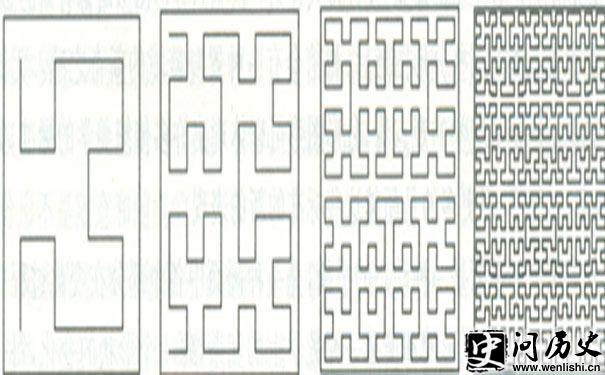
皮亚诺曲线
“1872年,康托在一篇文章中,用一章的篇幅专门讨论实数问题,特别是无理数问题。他为自己提出了一个目标,在不预先假定无理数存在的条件下,建立一个令人满意的无理数理论。显然,全体的有理数集合为此提供了一个基础。康托用有理数的无穷序列来定义无理数及它们之间的顺序关系。
从集合论的观点来看,由于数的序列对应的是数的集合,而不是数元素本身,即使形如只有一个元素的序列对应的也应该是一个数的集合。上面对有理数的定义显然构造了一个包含自指的集合:数a等于一个集合,这个集合中有一个元素,就是数a本身。这样的集合包含了罗素悖论。
有一点需要明确一下,就是无穷序列的构造过程以及对无穷序列取极限的过程的关系。我们已经知道[0,1]区间中有理数有可数无穷多个,可以用一个递归的无穷过程来产生这些有理数;而[0,1]区间中的无理数都是有理数集合的极限点。但有理数集和无理数集显然是不一样的。这就是说,构造有理数集的无穷过程并不包括取极限的过程,不能认为取极限的过程一定包含在无穷过程中。否则,按第一节的论述,对无理数的定义将包含罗素悖论。事实上,许多宣称找到了实数可数证据的例子都是犯了认为无穷过程一定包含取极限过程的错误。

皮亚诺曲线
另外,可以用反证法证明,希尔伯特曲线并没有建立一种从曲线到平面的一一对应关系。假设曲线的坐标区间为[0,1](即假设曲线的长度为1),并对于正方形中位线y轴上的某一点p,有曲线上的数x属于[0,1]映射到p点。由于希尔伯特曲线是左右对称的,则立即可以得到数(1-x)也映射到p点。又由于这种映射是一一映射,所以有x=1-x=1/2,即与1/2对应的是y轴上的一条线段,这与前面的一一对应假设矛盾。
这种观点指出,在康托用有理数的基本序列去定义实数中,实数域中的一个有理数a按定义等于序列,这实际上构造了一个包含自指的集合:数a等于一个集合,这个集合中有一个元素,就是数a本身。这样的集合包含了罗素悖论。
美女手机壁纸 〖寻图网〗

历史行业推荐公众号:历史阁楼公众号
更多有趣的历史,更多有趣的野史趣闻!欢迎扫描左方的二维码关注我们!公众号ID-(xue_lishi)
本文系作者授权本站发表,未经许可,不得转载。

推荐历史
Recommend article热门历史
HOT NEWS

